Rodding
Enigma Cryptanalysis home Page
Introduction
The Rodding method allows you to decipher a message encrypted with an Enigma. It requires knowing in advance the wiring of the rotors likely to be used in the Enigma and a Crib.
The method allows you to discover:
- The rotor used in the right position (the fast rotor).
- The starting position of this rotor.
- And finally, the continuation of the plain message that follows the Crib. This is obviously the goal of this method.
This method was invented in 1937 by Dilly Knox who was part of the English cryptological services. He used this method to decipher messages from the Francoists during the Spanish Civil War. The Enigma used by the Francoists was the commercial model but with a rewiring of the rotors. Dilly Knox had previously reconstituted the wiring of the rotors using another method that he invented, the "Button Up" method.
In 1938, the English services transmitted this method to the French, who called it "La méthode des bâtons". Before the declassification of the English archives, it was even believed that this method had been invented by the French.
The method
The principle
The great trick of the Rodding method is not needing to know the permutation performed by the reflector and the two slow rotors. For the sake of clarity, I will call this set (reflector and the two slow rotors), the extended reflector. This extended reflector can be considered static for each period of 26 letters (as long as the middle rotor does not advance).
Then we only use the encryption made at different positions of the fast rotor that associate one or more letters of the Crib (or cryptogram) always with the same letter that enters (or exits) the extended rotor. Thus the wiring of the extended rotor can be ignored (but only for a range of at most 26 letters).
In fact we use pairs of letters: a letter of the crib and the corresponding ciphered letter. These two letters are ciphered (or deciphered due to the reciprocity of the Enigma) at the same position of the fast rotor. We hope that other pairs of letters will use the same pair of letters that enters (or exits) the extended rotor but at different positions of the rotor. If this is the case, either we will check that the crib is correct, or (if the rotor position is beyond the crib), we find a new plain letter of the cryptogram.
Do not forget that as soon as the middle rotor turns, our reasoning no longer applies. We must (almost) start all over again.
Implementation in detail
The Rodding method consists of assembling pairs of rods. The two tested rods must belong to the same batch of 26 rods corresponding to a specific rotor. Since we first look for the rotor used, the rods of the same rotor are identified by a color. For example, the rods of rotor I are red, those of rotor II are pruple, and those of rotor III are green.
Each rod contains all the plain letters which for each rotor position (26 positions, therefore 26 letters) give the same encrypted letter.
We start with a cryptogram and a Crib. We therefore have a series of pairs (encrypted letter, plain letter) for different rotor positions. Unfortunately, we do not know the absolute value of the rotor position but only the relative positions. This is why we must try all possible positions: We assume that the first pair is in position 1, the second pair in position 1+1, etc. Then, in case of failure, we assume that the first pair is in position 2, the second in position 2+1, etc.
Let the following pairs be for the different positions (i) of the slow rotor:
position (i) 1 2 3 4 plain letter G O O D cipher letter X Z V V
We look for the two rods that encrypt G in X. We look for a first rod that contains the G in the first position (i=1), and another rod that at the same position gives X. Then for each correspondence between the letter of a rod that corresponds to a letter of the cryptogram, we enter it in our current hypothesis. If the correspondence is present in the crib there is either a confirmation or a contradiction. If the hypothesis is false, we move on to the next position, we test (G,X) in position 2, etc..
A complete example using our simplified Enigma
Introduction
We will use our simplified Enigma (link) for a first example .
Here is a cryptogram and a crib that gives the beginning of the plain message.
Position (i) 0 1 2 3 4 5 0 1 2 3 4 Cryptogram 5 0 4 4 2 1 5 1 5 4 2 Crib 2 4 0 1 ...
Creating the rods
The Rodding method requires knowing the wiring of the rotors likely to be in the right position (place of the fast rotor).
In the case of our simplified Enigma, we only have one rotor (it's simpler).
Here is the wiring of the Rotor and the reverse rotor:
R : 0 1 4 3 4 2 R reverse: 0 1 5 3 2 4
From these wirings, we create the encryption and decryption tables for the different positions of the rotor (given on the abscissa). Each line corresponds to the encrypted letter and at the line / column intersection, we have a plain letter.
Rotor Reverse Rotor
0 1 2 3 4 5 0 1 2 3 4 5
--------------- ---------------
0 | 0 0 2 0 1 3 0 | 0 0 3 0 4 5
1 | 1 3 1 2 4 1 1 | 1 4 1 5 0 1
2 | 4 2 3 5 2 2 2 | 5 2 0 1 2 2
3 | 3 4 0 3 3 5 3 | 3 1 2 3 3 0
4 | 5 1 4 4 0 4 4 | 2 3 4 4 1 4
5 | 2 5 5 1 5 0 5 | 4 5 5 2 5 3
Each rod actually corresponds to a line in the decryption table (Reverse Rotor). For example, rod 2: 5 2 0 1 2 2.
Deciphering text
We assume that for the first pair 5 /2 (plain letter / cipher letter), we are at position 0.
Notes:
- If we arrive at no deduction or if we have a contradiction, we will try position 2 and so on. If we have several Rotors, we test them in sequence.
- The method can fail if the crib is too short or if there is a turnover of the middle rotor. In our simplified Enigma, this is not possible (we have only one rotor).
We choose as first rod the one that has the letter 5 in position 0, that is to say rod 2. We choose as second rod the one that has the letter 2 in position 0, that is to say rod 4. Understand that the extended reflector (in the simplified Enigma, it is simply the reflector), encrypts 2 into 4.
We assemble the two rods and if a letter of one of the two rods corresponds to a ciphered letter or to a letter of the Crib in the same position, we have either a confirmation (if the position is in the Crib) or we deduce a new plain letter.
In our case, we have confirmations in positions 2 and 3 and we deduce new plain letters in positions 4, 0 and 4 (respectively 1, 2 and 1).
Pos. 0 1 2 3 4 5 0 1 2 3 4 (0)
Crypto 5 0 4 4 2 1 5 1 5 4 2
Crib 2 4 0 1 . . .
Rod 2 5 2 0 1 2 2 5 2 0 1 2 (1)
2 2 2 2 2 2 2 2 2 2 2 (2)
Rod 4 4 4 4 4 4 4 4 4 4 4 4 (3)
2 3 4 4 1 4 2 3 4 4 1 (4)
Match * * * * * *
Plain 2 0 1 1 2 1
- (0) The position of the rotor.
- (1) The plain letter at the input of the Rotor.
- (2) the corresponding letter at the output of the rotor and therefore at the input of the reflector.
- (3) The letter at the output of the reflector and therefore at the input of the rotor.
- (4) The letter at the output of the rotor, i.e. the encrypted letter.
Note: Due to the reciprocity of the Enigma, we can reverse the roles: in (4) we have the plain letter and in (1) the encrypted letter.
We now take the following pair, 0 / 4 in position 1:
Pos. 0 1 2 3 4 5 0 1 2 3 4
Crypto 5 0 4 4 2 1 5 1 5 4 2
Crib 2 4 0 1 . . .
Rod 0 0 0 3 0 4 5 0 0 3 0 4
0 0 0 0 0 0 0 0 0 0 0
Rod 1 1 1 1 1 1 1 1 1 1 1 1
1 4 1 5 0 1 1 4 1 5 0
Match * *
Plain 4 5
Me can deduce the plain letter 1 in position 5.
We have exhausted our Crib. We can no longer make any deductions.
In the end, we have confirmed our hypothesis (the rotor used, the rotor position and the crib). We have (this is the most important), reconstructed a part of the plain text that follows the Crib:
Pos. 0 1 2 3 4 5 0 1 2 3 4 Crypto 5 0 4 4 2 1 5 1 5 4 2 Crib 2 4 0 1 1 5 2 . . . 1
Note: In a realistic case with real letters (abcd...), one could have found the unfound plain letters by guessing words that included the found plain letters, For example: ..YPT...GY perhaps correpsond to CRYPTOLOGY.
A complete example using the military Enigma without steckers
Known (or assumed) information
We know the wiring of the three rotors of the Enigma. We will not use steckers.
Rotor I: - PI : EKMFLGDQVZNTOWYHXUSPAIBRCJ - Pi reverse: UWYGADFPVZBECKMTHXSLRINQOJ Rotor II: - PI : AJDKSIRUXBLHWTMCQGZNPYFVOE - PI reverse: AJPCZWRLFBDKOTYUQGENHXMIVS Rotor III: - PI : BDFHJLCPRTXVZNYEIWGAKMUSQO - PI reverse: TAGBPCSDQEUFVNZHYIXJWLRKOM
We have the following cryptogram:
QTUKS NSZFM CZRC UQPDZ MNDVB ZLUH
We assume it starts with the Crib "ourmachine".
Making rods
The rods are created using the following table. It corresponds to the encryption table of the reverse rotor I (which is equivalent to the decryption table)! As you can see, the first column corresponds to the reverse wiring of the rotor. The abscissa corresponds to the key (the rotor position) and the ordinate to the encrypted letter. A letter in the table corresponds to a plain letter.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A: U V W D W Y Z I N Q R T Q X Y E R G A S X N R T Q K B: W X E X Z A J O R S U R Y Z F S H B T Y O S U R L V C: Y F Y A B K P S T V S Z A G T I C U Z P T V S M W X D: G Z B C L Q T U W T A B H U J D V A Q U W T N X Y Z E: A C D M R U V X U B C I V K E W B R V X U O Y Z A H F: D E N S V W Y V C D J W L F X C S W Y V P Z A B I B G: F O T W X Z W D E K X M G Y D T X Z W Q A B C J C E H: P U X Y A X E F L Y N H Z E U Y A X R B C D K D F G I: V Y Z B Y F G M Z O I A F V Z B Y S C D E L E G H Q J: Z A C Z G H N A P J B G W A C Z T D E F M F H I R W K: B D A H I O B Q K C H X B D A U E F G N G I J S X A L: E B I J P C R L D I Y C E B V F G H O H J K T Y B C M: C J K Q D S M E J Z D F C W G H I P I K L U Z C D F N: K L R E T N F K A E G D X H I J Q J L M V A D E G D O: M S F U O G L B F H E Y I J K R K M N W B E F H E L P: T G V P H M C G I F Z J K L S L N O X C F G I F M N Q: H W Q I N D H J G A K L M T M O P Y D G H J G N O U R: X R J O E I K H B L M N U N P Q Z E H I K H O P V I S: S K P F J L I C M N O V O Q R A F I J L I P Q W J Y T: L Q G K M J D N O P W P R S B G J K M J Q R X K Z T U: R H L N K E O P Q X Q S T C H K L N K R S Y L A U M V: I M O L F P Q R Y R T U D I L M O L S T Z M B V N S W: N P M G Q R S Z S U V E J M N P M T U A N C W O T J X: Q N H R S T A T V W F K N O Q N U V B O D X P U K O Y: O I S T U B U W X G L O P R O V W C P E Y Q V L P R Z: J T U V C V X Y H M P Q S P W X D Q F Z R W M Q S P
Note that the diagonals (from top to bottom, from right to left) reproduce the wiring that connects the keyboard to the fast rotor (the ETW or Qwertzu). Since we use the military Enigma, the Qwertzu simply corresponds to the Identity permutation (ABCDE....Z).
A rod is neither more nor less than a line in this table.
Use of the method
 |
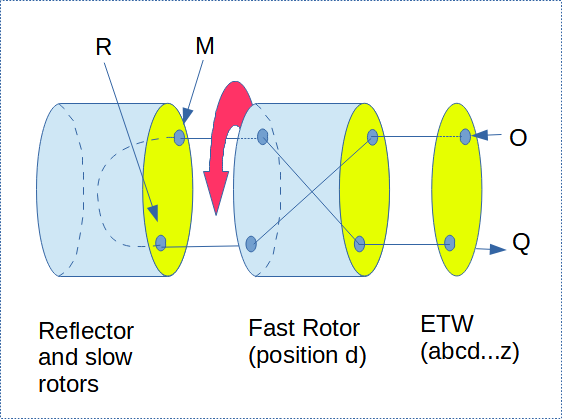Let's take the following cryptogram and Crib pair. We assume at the beginning that the key is A. If we arrive at no conclusion, we move on to the next key B and so on. At key D, we finally manage to find correspondences (Match) between several pairs (encrypted letter / crib letter).
Crypto: QTUKSNSZFMCZRCUQPDZMNDVBZLUH Crib: ourmachine.................. Key: abcdefghijklmnopqrstuvwxyzabcde... Rod R: XRJOEIKHBLMNUNPQZEHIKHOPVIXRJOE... Rod M: CJKQDSMEJZDFCWGHIPIKLUZCDFCJQDS... Match: * * *
Let us first assume that Rotor I is the fast rotor. If this assumption fails, we will test rotors II and III at the right position (that of the fast rotor).
Thanks to the pairs (Oq) and (Km) we can deduce that the letter n is in position L. The fact that we have two pairs that involve the letters of the Crib validates (statistically) that we have made the right choice of rotor, the right rods (R and M) and the right position.
Notes:
- We have swapped N and F because the Enigma is reciprocal.
- The fact that the Enigma is reciprocal prevents a letter from being encrypted by itself. This allows us to eliminate a supposed Crib and place a good Crib or also to be convinced that the Crib is good if it is long enough (several dozen characters).
Then we continue to scan the following pairs (Tu, Ur, ...) and each time we look for the corresponding rods to find new plain letters. We must obviously be careful that from a certain position of the rotor there will be a turnover of the middle rotor. We will have to determine the new key. If we can guess a word between the old key and the new one, we can easily continue our procedure. Otherwise, we will be stuck. We will have to find a new Crib.
Conclusion
In fact, we have not found any pair of rods that allow us to extend our Crib. I think Frank Carter (see link) was very lucky or he took a long time to create his example. I almost imitated him but I preferred to show a counterproductive example that shows that the Rodding method fails more often than one might think.
A complete example using the commercial Enigma
This case is very well described in Frank Carter's article (see Reference section).
Note: The ETW permutation of the Commercial Enigma isn't the Identity permutation, but it is equal to QWERTZUKIOASDFGHJKPYXCVBNML.
Frank Carter's article also describes in detail the consequences of turnover and how to manage it. In particular, it indicates the constraints that the middle rotor must respect.
Conclusion
The Rodding method invented by Dilly Knox is brilliant. It notably allowed Mavis Batey to decipher a message from the Italian Navy (which used the same rotors as the Francoists). This deciphering allowed Admiral Cunningham to win the great battle of Matapan in 1941.
But be careful, implementing this method is not easy. You need very good, very long cribs or several in-depth crib/cryptogram pairs. If the turnover of the middle rotor occurs too early, the deductions stop abruptly. Finally, it is a manual method that takes a lot of time. Especially since you don't have good cribs.
References
Books and articles
- Dilly, The Man Who Brake Enigmas, by Mavis Batey, Dialogue Editor, 2009. Appendix 2 : Rodding, by Frank Carter.
Internet links
- The Enigma Collection, Editor: Frode Weierud.
Rodding, by Frank Carter (link).